Default
QCI’s uniformly distributed Quantum Random Number Generator (uQRNG)
Carrie Spear, David Haycraft, Lac Nguyen, Helen Zhang, Yong Meng Sua
April 2023, v1.0
Introduction
Random number generation is the backbone of cryptography and an indispensable resource for a variety of applications, including the analysis of stochastic processes in the realms of physics, biology, finance, and as well as many other fields which require simulation and modeling. As the name implies, a random number is one that is selected by chance, or drawn from a set of numbers obeying a given distribution. A uniform random number must satisfy two requirements: the values are spread equally over a given range or set, and sample draws are independent of one another, meaning that the values of previous draws cannot be used to predict results of future samples. Pseudo-random number generators (PRNGs) produce random sequences based on mathematical algorithms and are therefore deterministic. In contrast, quantum random number generators (QRNGs) leverage the probabilistic nature of quantum mechanics, and can generate unbiased sequences of random numbers, from a non-deterministic process. Diverse physical phenomena have been utilized to implement QRNGs, including measurements of radioactive decay, vacuum noise, intrinsic phase fluctuation of lasers, energy fluctuation of stimulated Raman scattering, and superposition states of single photons. A novel photonic-based quantum random number generation method has been developed by Quantum Computing Inc. (QCI), which harvests randomness from the stochastic process of detecting single photons in superposition of time modes. QCI’s, uQRNG product, generates randomness with a uniform probability distribution over a discrete range.
The randomness of a sequence of numbers can be evaluated through the detection of patterns and biases. Various statistical testing methods are available for this purpose, including TestU01, PractRand, Diehard, Dieharder, and NIST tests. Using the uQRNG API that connects to the device via AWS, multiple sets of QRNs were collected. There is no industry standard specifically designed for testing quantum randomness. In order to test the quality of the quantum random numbers two well-known randomness test suites designed for cryptography, NIST (National Institute of Standards and Technology 2010) and Dieharder (Robert G. Brown 2023) were used to conduct rigorous evaluation of the randomness of uQRNG. This paper provides a description of QCI’s uQRNG, the conversion process of high-dimensional QRNs to binary, test results for QCI’s QRNG, and discusses future research for QRNGs at QCI.
Methods
QRNG theory of operation
The conceptional illustration of the RNG is depicted in Figure 1. QCI’s QRNG is quantum photonic based, the device harvests photons’ time-energy degree of freedom. Taking advantage of the discrete nature of photons, a low intensity monochromatic laser with constant intensity is used to generate sparse photon stream. The photon detections will follow a Poissonian statistic.
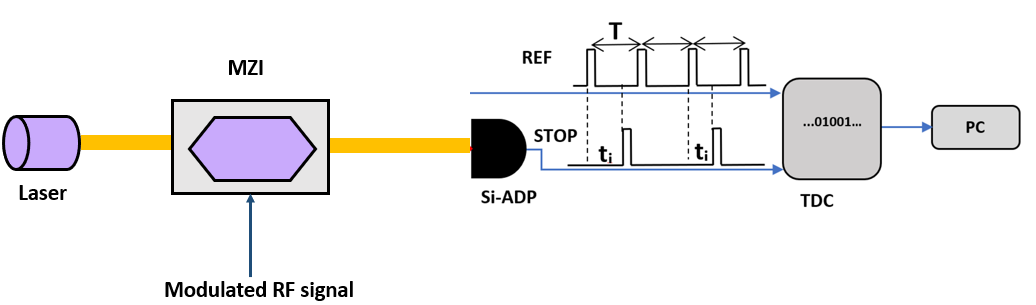
Before detection, a single photon is in superposition of the time modes, which means it is impossible to predict which state it will collapse into. The state vector of the photon before measurement is described as follows:
The true randomness of this quantum process can be obtained by measuring the stochastic arrival time of single photons compared to a reference clock. By modulating photon temporal waveform with customized shape using Mach-Zehnder interferometer (MZI), QCI’s QRNG can produce random series with arbitrary probability distribution, thus, for the first time, provides a direct physical method to generate non-uniform randomness in a controlled way. (Nguyen et al. 2018)
uQRNG
A uniform random number (uRN) is a random number where each possible number is equally likely to be produced as any other possible number across an evenly divided range. The uniform random number distribution generates numbers with equal probability within a given range. For example, uRNs are widely used in simulation-based studies to generate random inputs to test the performance of a system or to simulate a process. For instance, in a Monte Carlo simulation, uRNs are used to simulate the randomness of a process, such as the movement of particles in a system. Besides, uRN are used as entropy source in cryptography for cryptographic protocols. uRNs show their significance in optimization algorithms, where randomly generated candidate solutions should be unbiased and unpredictable.
QCI’s uQRNG operates without the modulation signal in order maintain uniformity. Given a time bins during a period, each photon detection is equally likely to fall in any bin, thus creating high-dimensional, uniform RN. Probability amplitude of each mode in equation ([superpos_equation]) become
Randomness study
Test suites
NIST Statistical Testing Suite (STS) version and Dieharder version 3.31.1 were performed to assess the uQRNG. Below are descriptions of each test.
| Test Name | Description |
|---|---|
| Test Name | Description |
| Frequency | This test determines whether the number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence (0s and 1s should each have a fraction of roughly 1/2) |
| Block Frequency | Tests that the proportion of zeroes and ones within M-bit blocks are close to M/2. |
| Runs | Tests whether the number of runs of ones and zeros of various lengths is as expected for a random sequence. |
| Longest Run | Tests sequence to determine if longest run is consistent with the length that would be expected in a random sequence. |
| Rank | This test checks for linear dependence among fixed length substrings of the original sequence. |
| FFT | Tests the spectral density of a sequence |
| Non-overlapping Template | Tests the frequency of non-overlapping substrings |
| Overlapping Template | Tests the frequency of overlapping substrings |
| Maurer’s Universal | Tests whether or not the sequence can be significantly compressed without loss of information. Too much compression indicates lack of randomness |
| Cumulative Sums | Tests for deviations from the mean in the cumulative sum of the sequence |
| Linear Complexity | Tests the complexity of a sequence, useful for detecting linear dependence which indicates non-randomness |
| Serial | Tests whether the number of occurrences of the m-bit overlapping patterns is approximately the same as would be expected for a random sequence |
| Approximate Entropy | Compares the frequency of overlapping blocks of two consecutive/adjacent lengths ( and ) against the expected result for a random sequence |
| Cumulative Sums | Determines whether the cumulative sum of the partial sequences occurring in the tested sequence is too large or too small relative to the expected behavior of that cumulative sum for random sequences (bits are mapped to and ). If sums stray too far from zero is considered non-random |
| Random Excursions | Determines if the number of visits to a state within a random walk exceeds what one would expect for a random sequence (bits are mapped to and ). |
| Random Excursions Variant | Detect deviations from the expected number of occurrences of various states in the random walk. |
| Test Name | Description |
|---|---|
| Test Name | Description |
| Diehard Birthdays | Each test determines the number of matching intervals from 512 “birthdays” (by default) drawn on a 24-bit “year” (by default). |
| Diehard OPERM5 | This test looks at a sequence of one million 32-bit random integers. Each set of five consecutive integers can be in one of 120 states, for the 5! possible orderings of five numbers. Thus the 5th, 6th, 7th, … numbers each provide a state. As many thousands of state transitions are observed, cumulative counts are made of the number of occurrences of each state. Then the quadratic form in the weak inverse of the covariance matrix yields a test equivalent to the likelihood ratio test that the 120 cell counts came from the specified (asymptotically) normal distribution with the specified covariance matrix (with rank 99). |
| Diehard Binary Rank | A random binary matrix is formed, each row a 32-bit random integer. The rank is determined. That rank can be from 0 to 32, ranks less than 29 are rare, and their counts are pooled with those for rank 29. Ranks are found for 40000 such random matrices and a chisquare test is performed on counts for ranks 32, 31, 30 and . |
| Diehard Binary Rank | From each of six random 32-bit integers from the generator under test, a specified byte is chosen, and the resulting six bytes form a binary matrix whose rank is determined. That rank can be from 0 to 6, but ranks 0, 1, 2, 3 are rare; their counts are pooled with those for rank 4. Ranks are found for 100000 random matrices, and a chi-square test is performed on counts for ranks 6, 5 and . |
| Diehard Bitstream | The file under test is viewed as a stream of bits. Call them , , …. Consider an alphabet with two “letters”, 0 and 1 and think of the stream of bits as a succession of 20-letter “words”, overlapping. Thus the first word is … , the second is … , and so on. The bitstream test counts the number of missing 20-letter (20-bit) words in a string of 2 to the 21 overlapping 20-letter words. |
| Diehard OPSO | Diehard Overlapping Pairs Sparse Occupance (OPSO) The OPSO test considers 2-letter words from an alphabet of 1024 letters. Each letter is determined by a specified ten bits from a 32-bit integer in the sequence to be tested. |
| Diehard OQSO | Similar to OPSO except that it considers 4-letter words from an alphabet of 32 letters, each letter determined by a designated string of 5 consecutive bits from the test file, elements of which are assumed 32-bit random integers. |
| Diehard DNA | The DNA test considers an alphabet of 4 letters:: C,G,A,T, determined by two designated bits in the sequence of random integers being tested. |
| Diehard Count the 1s (stream) | Consider the file under test as a stream of bytes (four per 32 bit integer). Each byte can contain from 0 to 8 1’s, with probabilities 1, 8, 28, 56, 70, 56, 28, 8, 1 over 256. Now let the stream of bytes provide a string of overlapping 5-letter words, each “letter” taking values A, B, C, D, E. The letters are determined by the number of 1’s in a byte:: 0, 1, or 2 yield A, 3 yields B, 4 yields C, 5 yields D and 6, 7 or 8 yield E. |
| Diehard Count the 1s | Consider the file under test as a stream of 32-bit integers. From each integer, a specific byte is chosen , say the left most:: bits 1 to 8. Each byte can contain from 0 to 8 1’s, with probabilities 1, 8, 28, 56, 70, 56, 28, 8, 1 over 256. Now let the specified bytes from successive integers provide a string of (overlapping) 5-letter words, each “letter” taking values A,B,C,D,E. The letters are determined by the number of 1’s, in that byte:: 0, 1, or 2 A, 3 B, 4 C, 5 D, and 6, 7 or 8 E. |
| Diehard Parking Lot | This tests the distribution of attempts to randomly park a square car of length 1 on a 100x100 parking lot without crashing. |
| Diehard Minimum Distance (2d Circle) | This test does this 100 times: choose random points in a square of side 10000. Find , the minimum distance between the “” pairs of points. |
| Diehard 3d Sphere (Minimum Distance) | Choose 4000 random points in a cube of edge 1000. At each point, center a sphere large enough to reach the next closest point. Then the volume of the smallest such sphere is (very close to) exponentially distributed with mean . Thus the radius cubed is exponential with mean 30. (The mean is obtained by extensive simulation). |
| Diehard Squeeze | Random integers are floated to get uniforms on . Start-ing with , the test finds , the number of iterations necessary to reduce to 1, using the reduction , with provided by floating integers from the file being tested |
| Diehard Sums | Integers are floated to get a sequence of uniform variables. Then overlapping sums, , are formed. The ’s are virtually normal with a certain covariance matrix. A linear transformation of the ’s converts them to a sequence of independent standard normals, which are converted to uniform variables for a KSTEST. The -values from ten KSTESTs are given still another KSTEST. |
| Diehard Runs | This test counts runs up, and runs down, in a sequence of uniform variables, obtained by floating the 32-bit integers in the specified file. This example shows how runs are counted: .123, .357, .789, .425, .224, .416, .95 contains an up-run of length 3, a down-run of length 2 and an up-run of (at least) 2, depending on the next values. |
| Diehard Craps | This test plays 200000 games of craps, finds the number of wins and the number of throws necessary to end each game. The number of wins should be (very close to) a normal with mean and variance , with . |
| Marsaglia and Tsang GCD | 10 to the 7 tsamples (default) of uint rands , are generated and two statistics are generated: their greatest common divisor (GCD) () and the number of steps of Euclid’s Method required to find it (). |
| STS Monobit | This test counts the 1 bits in a long
string of random uints. Compares to expected number, generates a
-value
directly from erfc(). |
| STS Runs | This test counts the total number of 0 runs + total number of runs across a sample of bits. |
| STS Serial | This test accumulates the frequencies of overlapping -tuples of bits drawn from a source of random integers. |
| RGB Bit Distribution | This test accumulates the frequencies of all tuples of bits in a list of random integers and compares the distribution thus generated with the theoretical (binomial) histogram, forming chisq and the associated -value. |
| RGB Generalized Minimum Distance | This is the generalized minimum distance
test, based on the paper of M. Fischler in the doc directory and private
communications. This test utilizes correction terms that are essential
in order for the test not to fail for large numbers of trials. It
replaces both “diehard_2dsphere.c” and
“diehard_3dsphere.c”, and generalizes the test itself so
that it can be run for any
. |
| RGB Permutations | This is a non-overlapping test that simply counts order permutations of random numbers, pulled out at a time. There are permutations and all are equally likely. |
| RGB Lagged Sum | Test for lagged correlations, the possibility that the RNG has a bitlevel correlation after some fixed number of intervening bits. |
| RGB Kolmogorov-Smirnov Test | This test generates a vector of tsamples uniform deviates from the selected rng, then applies an Anderson-Darling or Kuiper KS test to it to directly test for uniformity. |
Data preparation
(David: diagram and description for data processing process. Emphasize that we do not apply entropy amplification)
The data for the testing suite was obtained from the QRNG Application Programming Interface (API), which pulls from a cache of numbers that were created by QCI’s photonic uQRNG. Data samples consist of uniform bits, meaning that each bit has an equal probability of being 0 or 1. 845 million 32-bit samples were obtained by making requests using Python through uQRNG API version 0.0.1((QCI), n.d.). For more information on QCI’s uQRNG API see 5.
NIST STS version 2.1.2 and Dieharder version 3.31.1 were performed to assess the uQRNG. The same set of 845 million 32-bit samples was used for both testing suites. The NIST STS is a set of 15 statistical tests that are meant to detect randomness in binary sequences. In this test suite, each of the individual tests was executed 10 times. 10-bit streams were used for all tests to determine the -values. The assess value, which is defined as “the number of bits to test in one test run,” was set to 387840. Each of NISTs tests is considered to have passed if conforms to . The Dieharder suite consists of 19 tests and demands a larger dataset than NIST to carry out a comprehensive evaluation. The Kolmogorov Smirnov (KS) test is employed by Dieharder to assess the -value distribution, which is highly sensitive to lack of uniformity. Uniformly high -values or low -values both indicate bias in the testing results for a given RNG. Each test is run 100 times to ensure that the resolution is high enough to assess lack of uniformity in the -values. The default threshold value of defines a WEAK result and is a FAILED result. Although the Dieharder documentation does not provide guidelines for sample size for analyzing random numbers, according to Hurley-Smith (Hurley-Smith and Hernandez-Castro 2021), their work indicates, a minimum of 228 GB of 32-bit data is necessary to avoid data rewinding during testing. Due to the unavailability of sufficient data during the data collection period, Dieharder was run with rewinds of the random numbers to obtain the results.
Results
Using the test settings as described above each NIST test all 15 tests passed with -values greater than 0.01. The tests included in the suite are designed to detect a wide range of deviations from randomness, such as biases, patterns, and correlations, and the generator demonstrated robustness against all of these potential weaknesses.
Dieharder similarly passed all 19 tests without any significant failures. However, some runs did have WEAK individual -values. STS serial had 3 WEAK -values over the course of its 29 runs. RGB lagged sum had one WEAK -value across the 33 runs. Conducting Dieharder with more samples and higher total number of tests may provide more insight into these result. This may be considered to be part of the random fluctuations in the underlying test statistic and stronger weight should be given to the passing results on this harder battery of tests indicating the high quality of the random numbers from the uQRNG.
Discussion
In conducting randomness tests, it is not uncommon to observe some failures due to random chance. To mitigate this phenomenon, adjustments such as analyzing multiple tests and observing the distribution of -values were employed (Rukhin et al. 2010). The sample size used in this study was adequate to pass the randomness testing suites, as all tests yielded -values above the significance threshold. However, it is worth noting that for the Dieharder test suite, a larger sample size may have been preferable to reduce the need for rewinding during testing. This would have provided a more accurate assessment of the generator’s randomness properties. Nonetheless, the sample size used in this study was still deemed sufficient to provide a reliable evaluation of the generator’s performance. While true randomness cannot be replicated exactly, similar test settings should yield comparable results.
The tests suites employed to analyze the random numbers employ a variety of statistical tests to analyze the input sequences. Nevertheless, these tests are not infallible, and it is possible to construct a set of numbers that could deliberately pass these tests and give the impression of being random. There was no manipulation of the numbers employed beyond what is described within 5.
Quantum Computing Inc’s uQRNG device generates high-quality numbers which can pass the most stringent tests available without any randomness extraction to alleviate bias or randomness amplification to increase entropy. Given the true randomness inherent in the underlying quantum mechanical processes, the QRNG used in this study is well-suited for entropy source of cryptographic protocols. Furthermore, the lack of bias exhibited by the generator may also prove advantageous for generating random numbers for other applications such as experiments and simulations that require unbiased and truly random results. Future research will explore the potential benefits of using this generator for real-world experimentation in modeling, simulation, and cryptographic applications.
DieHarder and NIST are two of many possible randomness tests. Testing using other suites may be desirable to further validate the generator’s performance. QCI is committed to conducting all necessary statistical tests and standards to support existing and future customer applications.The future development of QRNG devices by QCI includes random numbers certified by non-local correlations of quantum states by the means of violation of Bell’s inequality beyond standard statistical randomness test suite. The violation of Bell’s inequality guarantees that the correlated random numbers generated from quantum entangled systems possess intrinsic randomness.
QCI’s QRNG API
The QCI QRNG API supports a variety of formats and distributions. Samples are read directly from the device, and the raw output is processed via time-binning and ranging to create a specified number of bits. In the current generation of the QRNG, each of the measurement bins represents 100 picoseconds. 90,300 picoseconds are censored from the start and the end of the detection interval when obtaining samples. Each sample is a 13-bit uniform random number. These bits are then cached until a request is made that uses them, after which they are deleted to prevent reuse.
To use the API, registration with QCI is required, and an access token is needed to access the service. Each request is limited to acquiring one million numbers, which can be returned as either numbers or binary strings. For testing purposes, binary strings were used to provide the appropriate input format for NIST and Dieharder. Consecutive samples were concatenated together to produce 32 bit samples.
- import requests
- BEARER_TOKEN = "YOUR_BEARER_TOKEN"
- QRNG_URL = "https://api.qci-next.com/qrng/random_numbers"
- headers = {"Authorization": f"Bearer {BEARER_TOKEN}"}
- result = requests.post(f"{ip_address}/random_numbers",
- json = {"distribution": "uniform_discrete",
- "n_samples": 10**6,
- "n_bits": 16,
- "output_type": "binary"},
- headers = headers)
For further information on API please see API Quickstart Guide((QCI), n.d.).
References
- Hurley-Smith, Darren, and Julio Hernandez-Castro. 2021. “Challenges in Certifying Small-Scale (IoT) Hardware Random Number Generators.” In Security of Ubiquitous Computing Systems: Selected Topics, edited by Gildas Avoine and Julio Hernandez-Castro, 165–81. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-10591-4_10.
- National Institute of Standards and Technology. 2010. “Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications.” https://csrc.nist.gov/projects/random-bit-generation/documentation-and-software.
- Nguyen, Lac, Patrick Rehain, Yong Meng Sua, and Yu-Ping Huang. 2018. “Programmable Quantum Random Number Generator Without Postprocessing.” Opt. Lett. 43 (4): 631–34. https://doi.org/10.1364/OL.43.000631.
- (QCI), Quantum Computing Inc. n.d. “QCI QRNG API Guide.” https://quantumcomputinginc.com/qrng/api-guide/.
- Robert G. Brown. 2023. “Dieharder: A Random Number Test Suite.” https://webhome.phy.duke.edu/~rgb/General/dieharder.php.
- Rukhin, Andrew, Juan Soto, James Nechvatal, Miles Smid, Elaine Barker, Stefan Leigh, Mark Levenson, et al. 2010. “A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications.” SP 800-22 Rev. 1a. National Institute of Standards; Technology (NIST). https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22r1a.pdf.